Системой неравенств принято называть любую совокупность двух или более неравенств, содержащих неизвестную величину.

Наглядно данную формулировку иллюстрируют, к примеру, такие системы неравенств :

Решить систему неравенств - означает найти все значения неизвестной переменной, при которых реализуется каждое неравенство системы, либо обосновать, что таких не бывает.

Значит, для каждого отдельного неравенства системы вычисляем неизвестную переменную. Далее из получившихся значений выбирает только те, которые верны и для первого и для второго неравенства. Следовательно, при подстановке выбранного значения оба неравенства системы становятся правильными.

Разберем решение нескольких неравенств:

Разместим одну под другой пару числовых прямых; на верхнею нанесем величину x , при которых первое неравенств о (x > 1) становиться верным, а на нижней—величину х , которые являются решением второго неравенства (х > 4).

Сопоставив данные на числовых прямых , отметим, что решением для обоих неравенств будет х > 4. Ответ, х > 4.

Пример 2.

Вычисляя первое неравенство получаем -3х < -6, или x > 2, второе -х > -8, или х < 8. Затем делаем по аналогии с предыдущим примером. На верхнюю числовую прямую наносим все те значения х , при которых реализуется первое неравенство системы , а на нижнюю числовую прямую, все те значения х , при которых реализуется второе неравенство системы.

Сопоставив данные, получаем, что оба неравенства будут реализовываться при всех значениях х , размещенных от 2 до 8. Множеств значений х обозначаем двойным неравенством 2 < х < 8.

Пример 3. Найдем

называется любая совокупность двух или более линейных неравенств, содержащих одну и туже неизвестную величину

Вот образцы подобных систем:

Промежуток пересечения двух лучей и есть наше решение. Следовательно решением данного неравенства выступают все х расположенные между двойкой и восьмеркой.

Ответ: х

Применение такого типа отображения решения системы неравенств иногда именуют методом крыш .

Определение: Пересечением двух множеств А и В называется такое третье множество, которое включает все элементы, входящих и в А и в В . Это смысл пересечения множеств произвольной природы. Нами сейчас детально рассматриваются числовые множества, поэтому при нахождении линейных неравенств такими множествами являются лучи - сонаправленные, противонаправленные и так далее.

Выясним на реальных примерах нахождение линейных систем неравенств, как определить пересечения множеств решений отдельных неравенств, входящих в систему.

Вычислим систему неравенств :

Поместим одну под другой две силовые прямые. На верхней нанесем те значения х, которые выполняют первое неравенство x >7 , а на нижней - которые выступают решением второго неравенства x >10 Соотнесем результаты числовых прямых, выясним, что оба неравенства будут удовлетворятся при x >10.

Ответ: (10;+∞).

Делаем по аналогии с первым образцом. На заданной числовой оси наносим все те значения х при которых существует первое неравенство системы , а на второй числовой оси, размещенной под первой, - все те значения х , при которых выполняется второе неравенство системы. Соотнесем эти два результата и определим, что оба неравенства одновременно будут выполнятся при всех значениях х расположенных между 7 и 10 с учетом знаков получаем 7<х≤10

Ответ: (7; 10].

Подобным образом решаются и нижеследующие системы неравенств.

Неравенство - это два числа или математических выражения, соединённых одним из знаков: > (больше, в случае строгих неравенств), < (меньше, в случае строгих неравенств), ≥ (больше или равно, в случае нестрогих неравенств), ≤ (меньше или равно, в случае нестрогих неравенств).

Неравенство является линейным при тех же условиях, что и уравнение: оно содержит переменные только в первой степени и не содержит произведений переменных.

Решение линейных неравенств и систем линейных неравенств неразрывно связано с их геометрическим смыслом: решением линейного неравенства является некоторая полуплоскость, на которые всю плоскость делит прямая, уравнением которой задано линейное неравенство. Эту полуплоскость, а в случае системы линейных неравенств - часть плоскости, ограниченную несколькими прямыми, требуется найти на чертеже.

К решению систем линейных неравенств с большим числом переменных сводятся многие экономические задачи, в частности, задачи линейного программирования , в которых требуется найти максимум или минимум функции.

Решение систем линейных неравенств с любым числом неизвестных

Сначала разберём линейные неравенства на плоскости. Рассмотрим одно неравенство с двумя переменными и :

,

где - коэффициенты при переменных (некоторые числа), - свободный член (также некоторое число).

Одно неравенство с двумя неизвестными, так же как и уравнение, имеет бесчисленное множество решений. Решением данного неравенства назовём пару чисел , удовлетворяющих этому неравенству. Геометрически множество решений неравенства изображается в виде полуплоскости, ограниченной прямой

,

которую назовём граничной прямой.

Шаг 1. Построить прямую, ограничивающую множество решений линейного неравенства

Для этого надо знать какие-либо две точки этой прямой. Найдём точки пересечения с осями координат. Ордината точки пересечения A равна нулю (рисунок 1). Числовые значения на осях на этом рисунке относятся к примеру 1, который разберём сразу после этого теретического экскурса.

Абсциссу найдём, решая как систему уравнение прямой с уравнением оси .

Найдём пересечение с осью :

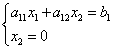
Подставляя значение в первое уравнение, получаем

Откуда .

Таким образом, нашли абсциссу точки A .

Найдём координаты точки пересечения с осью .

Абсцисса точки B равна нулю. Решим уравнение граничной прямой с уравнением оси координат:

,

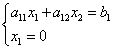
следовательно, координаты точки B : .

Шаг 2. Начертить прямую, ограничивающую множество решений неравенства. Зная точки A и B пересечения граничной прямой с осями координат, можем начертить эту прямую. Прямая (снова рисунок 1) делит всю плоскость на две части, лежащие справа и слева (выше и ниже) от этой прямой.

Шаг 3. Установить, которая из полуплоскостей является решением данного неравенства. Для этого нужно в это неравенство подставить начало координат (0; 0). Если координаты начала удовлетворяют неравенству, то решением неравенства является полуплоскость, в которой находится начало координат. Если же координаты не удовлетворяют неравенству, то решением неравенства является полуплоскость, которая не содержит начала координат. Полуплоскость решения неравенства будем обозначать штрихами от прямой внутрь полуплоскости, как на рисунке 1.

Если решаем систему линейных неравенств , то каждый шаг выполняется для каждого из неравенств системы.

Пример 1. Решить неравенство

Решение. Начертим прямую

Подставив в уравнение прямой , получим , а подставив , получим . Следовательно, координаты точек пересечения с осями будут A (3; 0) , B (0; 2) . Через эти точки проведём прямую (опять рисунок 1).

Выберем полуплоскость решений неравенства. Для этого в неравенство подставим координаты начала (0; 0) :

получим , т. е. координаты начала удовлетворяют данному неравенству. Следовательно, решением неравенства является полуплоскость, содержащая в себе начало координат, т. е. левая (она же нижняя) полуплоскость.

Если бы данное неравенство было строгим, то есть имело бы вид

то точки граничной прямой не являлись бы решением, так как они не удовлетворяют неравенству.

Теперь рассмотрим систему линейных неравенств с двумя неизвестными:

Каждое из неравенств этой системы на плоскости определяет полуплоскость. Система линейных неравенств называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет решений. Решением системы линейных неравенств называется любая пара чисел (), удовлетворяющая всем неравенствам данной системы.

Геометрически решением системы линейных неравенств является множество точек, удовлетворяющих всем неравенствам системы, то есть, общая часть получаемых полуплоскостей. Поэтому геометрически в общем случае решение может быть изображено в виде некоторого многоугольника, в частном случае - может быть линия, отрезок и даже точка. Если система линейных неравенств несовместна, то на плоскости не существует ни одной точки, удовлетворяющей всем неравенствам системы.

Пример 2.

Решение. Итак, требуется найти многоугольник решений этой системы неравенств. Построим граничную прямую для первого неравенства, то есть прямую , и граничную прямую для второго неравенства, то есть прямую .

Делаем это пошагово, как было показано в теоретической справке и в примере 1, тем более, что в примере 1 строили граничную прямую для неравенства, которое является первым в данной системе.

Полуплоскости решений, соответствующие неравенствам данной системы, на рисунке 2 заштрихованы вовнутрь. Общая часть полуплоскостей решений представляет собой открытый угол ABC . Это означает, что множество точек плоскости, составляющих открытый угол ABC , является решением как первого, так и второго неравенства системы, то есть, является решением системы двух линейных неравенств. Иначе говоря, кординаты любой точки из этого множества удовлетворяют обоим неравенствам системы.

Пример 3. Решить систему линейных неравенств

Решение. Построим граничные прямые, соответствующие неравенствам системы. Делаем это, выполняя шаги, данные в теоретической справке, для каждого неравенства. Теперь определим полуплоскости решений для каждого неравенства (рисунок 3).

Полуплоскости решений, соответствующие неравенствам данной системы, заштрихованы вовнутрь. Пересечение полуплоскостей решений изображается, как показано на рисунке, в виде четырёхугольника ABCE . Получили, что многоугольник решений системы линейных неравенств с двумя переменными является четырёхугольником ABCE .

Всё описанное выше о системах линейных неравенств с двумя неизвестными относится и к системе неравенств с любым числом неизвестных, с той лишь разницей, что решением неравенства с n неизвестными будет совокупность n чисел (), удовлетворяющих всем неравенствам, а вместо граничной прямой будет граничная гиперплоскость n -мерного пространства. Решением будет многогранник решений (симплекс), ограниченный гиперплоскостями.

Программа для решения линейных, квадратных и дробных неравенств не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс решения для того чтобы проконтролировать знания по математике и/или алгебре.

Причём, если в процессе решения одного из неравенств нужно решить, например, квадратное уравнение, то его подробное решение также выводится (оно заключается в спойлер).

Данная программа может быть полезна учащимся старших классов при подготовке к контрольным работам, родителям для контроля решения неравенств их детьми.

Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Правила ввода неравенств

В качестве переменной может выступать любая латинсая буква.
Например: \(x, y, z, a, b, c, o, p, q \) и т.д.

Числа можно вводить целые или дробные.
Причём, дробные числа можно вводить не только в виде десятичной, но и в виде обыкновенной дроби.

Правила ввода десятичных дробей.
В десятичных дробях дробная часть от целой может отделяться как точкой так и запятой.
Например, можно вводить десятичные дроби так: 2.5x - 3,5x^2

Правила ввода обыкновенных дробей.
В качестве числителя, знаменателя и целой части дроби может выступать только целое число.

Знаменатель не может быть отрицательным.

При вводе числовой дроби числитель отделяется от знаменателя знаком деления: /
Целая часть отделяется от дроби знаком амперсанд: &
Ввод: 3&1/3 - 5&6/5y +1/7y^2
Результат: \(3\frac{1}{3} - 5\frac{6}{5} y + \frac{1}{7}y^2 \)

При вводе выражений можно использовать скобки. В этом случае при решении неравенства выражения сначала упрощаются.
Например: 5(a+1)^2+2&3/5+a > 0,6(a-2)(a+3)

Выберите нужный знак неравенства и введите многочлены в поля ниже.

Первое неравенство системы.

Нажмите на кнопку для изменения типа первого неравенства.

> >= < <=

Решить систему неравенств

Обнаружено что не загрузились некоторые скрипты, необходимые для решения этой задачи, и программа может не работать.
Возможно у вас включен AdBlock.
В этом случае отключите его и обновите страницу.

У вас в браузере отключено выполнение JavaScript.
Чтобы решение появилось нужно включить JavaScript.
Вот инструкции, как включить JavaScript в вашем браузере .

Т.к. желающих решить задачу очень много, ваш запрос поставлен в очередь.
Через несколько секунд решение появится ниже.
Пожалуйста подождите сек...

Если вы заметили ошибку в решении , то об этом вы можете написать в Форме обратной связи .
Не забудте указать какую задачу вы решаете и что вводите в поля .

Наши игры, головоломки, эмуляторы:

Немного теории.

Системы неравенств с одним неизвестным. Числовые промежутки

С понятием системы вы познакомились в 7 классе и научились решать системы линейных уравнений с двумя неизвестными. Далее будут рассмотрены системы линейных неравенств с одним неизвестным. Множества решений систем неравенств могут записываться с помощью промежутков (интервалов, полуинтервалов, отрезков, лучей). Также вы познакомитесь обозначениями числовых промежутков.

Если в неравенствах \(4x > 2000 \) и \(5x \leq 4000 \) неизвестное число х одно и то же, то эти неравенства рассматривают совместно и говорят, что они образуют систему неравенств: $$ \left\{\begin{array}{l} 4x > 2000 \\ 5x \leq 4000 \end{array}\right. $$

Фигурная скобка показывает, что нужно найти такие значения х, при которых оба неравенства системы обращаются в верные числовые неравенства. Данная система - пример системы линейных неравенств с одним неизвестным.

Решением системы неравенств с одним неизвестным называется то значение неизвестного, при котором все неравенства системы обращаются в верные числовые неравенства. Решить систему неравенств - это значит найти все решения этой системы или установить, что их нет.

Неравенства \(x \geq -2 \) и \(x \leq 3 \) можно записать в виде двойного неравенства: \(-2 \leq x \leq 3 \).

Решениями систем неравенств с одним неизвестным являются различные числовые множества. Эти множества имеют названия. Так, на числовой оси множество чисел х, таких, что \(-2 \leq x \leq 3 \), изображается отрезком с концами в точках -2 и 3.

-2

3

Если \(a отрезком и обозначается [а; b]

Если \(a интервалом и обозначается (а; b)

Множества чисел \(x \), удовлетворяющих неравенствам \(a \leq x полуинтервалами и обозначаются соответственно [а; b) и (а; b]

Отрезки, интервалы, полуинтервалы и лучи называют числовыми промежутками .

Таким образом, числовые промежутки можно задавать в виде неравенств.

Решением неравенства с двумя неизвестными называется пара чисел (х; у), обращающая данное неравенство в верное числовое неравенство. Решить неравенство - это значит найти множество всех его решений. Так, решениями неравенства х > у будут, например, пары чисел (5; 3), (-1; -1), так как \(5 \geq 3 \) и \(-1 \geq -1\)

Решение систем неравенств

Решать линейные неравенства с одним неизвестным вы уже научились. Знаете, что такое система неравенств и решение системы. Поэтому процесс решения систем неравенств с одним неизвестным не вызовет у вас затруднений.

И все же напомним: чтобы решить систему неравенств, нужно решить каждое неравенство по отдельности, а затем найти пересечение этих решений.

Например, исходная система неравенств была приведена к виду:
$$ \left\{\begin{array}{l} x \geq -2 \\ x \leq 3 \end{array}\right. $$

Чтобы решить эту систему неравенств, отметим решение каждого неравенства на числовой оси и найдём их пересечение:

-2

3

Пересечением является отрезок [-2; 3] - это и есть решение исходной системы неравенств.

Рассмотрим на примерах, как решить систему линейных неравенств.

4x + 29 \end{array} \right.\]" title="Rendered by QuickLaTeX.com">

Чтобы решить систему, нужно каждое из составляющих её неравенств. Только решение принято записывать не по отдельности, а вместе, объединяя их фигурной скобкой.

В каждом из неравенств системы неизвестные переносим в одну сторону, известные — в другую с противоположным знаком:

Title="Rendered by QuickLaTeX.com">

После упрощения обе части неравенства надо разделить на число, стоящее перед иксом. Первое неравенство делим на положительное число, поэтому знак неравенства не изменяется. Второе неравенство делим на отрицательное число, поэтому знак неравенства надо изменить на противоположный:

Title="Rendered by QuickLaTeX.com">

Решение неравенств отмечаем на числовых прямых:

В ответ записываем пересечение решений, то есть ту часть, где штриховка есть на обеих прямых.

Ответ: x∈[-2;1).

В первом неравенстве избавимся от дроби. Для этого обе части умножим почленно на наименьший общий знаменатель 2. При умножении на положительное число знак неравенства не изменяется.

Во втором неравенстве раскрываем скобки. Произведение суммы и разности двух выражений равно разности квадратов этих выражений. В правой части — квадрат разности двух выражений.

Title="Rendered by QuickLaTeX.com">

Неизвестные переносим в одну сторону, известные — в другую с противоположным знаком и упрощаем:

Обе части неравенства делим на число, стоящее перед иксом. В первом неравенстве делим на отрицательное число, поэтому знак неравенства изменяется на противоположный. Во втором — делим на положительное число, знак неравенства не изменяется:

Title="Rendered by QuickLaTeX.com">

Оба неравенства со знаком «меньше» (не существенно, что один знак — строго «меньше», другой — нестрогий, «меньше либо равно»). Можем не отмечать оба решения, а воспользоваться правилом « «. Меньшим является 1, следовательно, система сводится к неравенству

Отмечаем его решение на числовой прямой:

Ответ: x∈(-∞;1].

Раскрываем скобки. В первом неравенстве — . Оно равно сумме кубов этих выражений.

Во втором — произведение суммы и разности двух выражений, что равно разности квадратов. Поскольку здесь перед скобками стоит знак «минус», лучше их раскрытие провести в два этапа: сначала воспользоваться формулой, а уже потом раскрывать скобки, меняя знак каждого слагаемого на противоположный.

Переносим неизвестные в одну сторону, известные — в другую с противоположным знаком:

Title="Rendered by QuickLaTeX.com">

Оба знака «больше». Используя правило «больше большего», сводим систему неравенств к одному неравенству. Большее из двух чисел 5, следоветельно,

Title="Rendered by QuickLaTeX.com">

Решение неравенства отмечаем на числовой прямой и записываем ответ:

Ответ: x∈(5;∞).

Поскольку в алгебре системы линейных неравенств встречается не только в качестве самостоятельных заданий, но и в ходе решения разного рода уравнений, неравенств и т.д., важно вовремя усвоить эту тему.

В следующий раз мы рассмотрим примеры решения систем линейных неравенств в частных случаях, когда одно из неравенств не имеет решений либо его решением является любое число.

Рубрика: |